Çemberde Açılar Formülleri

 DERS KİTABI CEVAPLARINA BURADAN ULAŞABİLİRSİNİZ! 

Çemberde Açılar Formülleri

Çemberde açılar konusu formülleri, çemberde açı özellikleri, örnek soru çözümleri, özel durumlar ve kolaylaştırıcı ipuçları

Çemberde Açılar

Çemberde Açı Çeşitleri

Merkez Açı: Köşesi çemberin merkezinde olan açıdır. Merkez açının ölçüsü, gördüğü yayın ölçüsüne eşittir.

Çemberde Açılar Formülleri

\displaystyle m\widehat{AOB}=m\overset\frown{AB}

Çevre Açı:

Köşesi çember üzerinde olan iki kirişin oluşturduğu açıya denir. Çevre açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir.

\displaystyle m\left( \widehat{BAC} \right)=\frac{m\overset\frown{\left( BC \right)}}{2}

Aynı yayı gören çevre açıların ölçüleri birbirine eşittir.

\displaystyle m\left( \widehat{BAC} \right)=m\left( \widehat{BDC} \right)=\frac{m\overset\frown{\left( BC \right)}}{2}=\alpha 

Çapı gören çevre açılar diktir.

\displaystyle \left[ AB \right] çap ise

\displaystyle m\left( \widehat{ACB} \right)={{90}^{\circ }}

\displaystyle m\left( \widehat{ADB} \right)={{90}^{\circ }}

\displaystyle m\left( \widehat{AEB} \right)={{90}^{\circ }}

Teğet, değme noktasından ve merkezden geçen doğruya diktir.

Bir çemberin herhangi bir noktasındaki teğetine merkezden ve teğet noktasından geçen bir doğru çizilirse bu doğru ile teğet doğru dik kesişir çemberin merkezinden ve teğet noktasından geçen bu doğruya çemberin normali denir.

Şekildeki d doğrusu, çemberin T noktasından geçen normalidir.

Teğet – Kiriş Açı:

Köşesi çember üzerinde olup, kollarından biri çemberin teğeti, diğeri çemberin kirişi olan açıya teğet kiriş açı denir.Teğet kiriş açının ölçüsü, gördüğü yayın ölçüsünün yarısına eşittir.

\displaystyle m\left( \widehat{LAB} \right)=\alpha 

teğet kiriş açı

\displaystyle m\left( \overset\frown{AB} \right)=2\alpha 

\displaystyle m\left( \widehat{LAB} \right)=\frac{m\left( \overset\frown{AB} \right)}{2}

Aynı yayı gören teğet kiriş açının ölçüsü ile çevre açının ölçüsü birbirine eşittir.

\displaystyle m\left( \widehat{ABC} \right)=m\left( \widehat{CAD} \right)=\frac{m\left( \overset\frown{AC} \right)}{2}=\alpha 

Aynı yayı gören teğet kiriş açıların ölçüleri birbirine eşittir.

\displaystyle m\left( \widehat{KAB} \right)=m\left( \widehat{LBA} \right)

İç Açı : Bir çemberin kesişen iki kirişi arasındaki açıya iç açı denir.

İç açının ölçüsü, gördüğü yayların ölçüleri toplamının yarısına eşittir.

\displaystyle m\left( \widehat{DEC} \right)=\alpha 

\displaystyle \alpha =\frac{m\left( \overset\frown{AB} \right)+m\left( \overset\frown{CD} \right)}{2}

\displaystyle m\left( \overset\frown{AB} \right)=2a

\displaystyle m\left( \overset\frown{DC} \right)=2b

\displaystyle \alpha =a+b

Dış Açı :Çemberin dış bölgesinde kesişen iki kesenin oluşturduğu açıya dış açı denir, ölçüsü gördüğü yayların farkının yarısına eşittir.

\displaystyle \beta =\frac{m\left( \overset\frown{AB} \right)-m\left( \overset\frown{CD} \right)}{2}

\displaystyle m\left( \overset\frown{AB} \right)=2a

\displaystyle m\left( \overset\frown{CD} \right)=2b

\displaystyle a=b+\beta \Rightarrow \beta =a-b

UYARI

Dış açı, çemberin bir kesen ve bir teğetinin kesişmesiyle de oluşur.

Dış açı, çemberin iki teğetinin kesişmesiyle de oluşur. Oluşan dış açının ölçüsü ile gördüğü yayın ölçüsü toplamı 180° dir.

\displaystyle m\left( \overset\frown{AC} \right)+m\left( \widehat{ABC} \right)={{180}^{{}^\circ }}

\displaystyle m\left( \overset\frown{AC} \right)={{180}^{{}^\circ }}-\beta 

\displaystyle m\left( \overset\frown{ADC} \right)={{180}^{{}^\circ }}+\beta 

[OA] ve [OC] çizilirse [OA]⊥[BA, [OC]⊥[BC olur.

\displaystyle m\left( \overset\frown{AC} \right)=m\left( \widehat{AOC} \right)=\alpha 

AOCB dörtgeninde;

α+β+90°+90° = 360° ⇒ α +β = 180°

UYARI

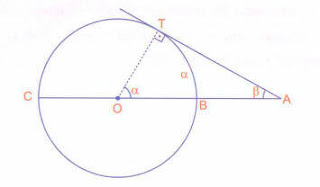
Bir dış açı, çemberin bir teğeti ve merkezinden geçen keseni arasında ise, dış açı ölçüsü ile gördüğü yayın ölçüsü toplamı 90° dir.

\displaystyle m\left( \widehat{TAC} \right)+m\left( \overset\frown{TB} \right)={{90}^{\circ }}

\displaystyle m\left( \widehat{TOB} \right)=m\left( \overset\frown{TB} \right)=\alpha 

TOA üçgeninde; α +β = 90°

UYARI

*** İç açı ölçüsü ile dış açı ölçüsü toplamı, büyük yay ölçüsünü verir.\displaystyle m\left( \overset\frown{AB} \right)=\alpha +\beta 

** İç açı ölçüsü ile dış açı ölçüsü farkı, küçük yay ölçüsünü verir.

 DERS VE ÇALIŞMA KİTABI CEVAPLARINA BURADAN ULAŞABİLİRSİNİZ